An Intelligent Policy System for Channel Allocation of Information Appliance

Cheng-Yuan Ku; Chang-Jinn Tsao; David Yen

doi:10.6180/jase.2002.5.1.08

An Intelligent Policy System for Channel Allocation of Information Appliance

Computer Science and Information Engineering

Cheng-Yuan Ku This email address is being protected from spambots. You need JavaScript enabled to view it.¹ , Chang-Jinn Tsao This email address is being protected from spambots. You need JavaScript enabled to view it.² and David Yen This email address is being protected from spambots. You need JavaScript enabled to view it.³

¹Department of Information Management National Chung Cheng University Chia-Yi County, Taiwan 600, R.O.C.
²Embedded Systems Laboratory Institute for Information Industry Taipei, Taiwan 106, R.O.C.
³Department of Decision Sciences and Management Information Systems Miami University Oxford, Ohio 45056, U.S.A.

Received: October 30, 2001
Accepted: February 20, 2002
Publication Date: March 1, 2002

Download Citation: ||https://doi.org/10.6180/jase.2002.5.1.08

ABSTRACT

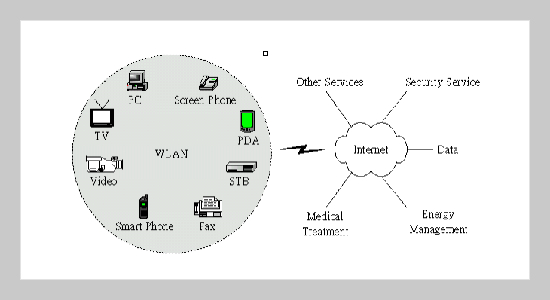
In this paper, we propose a closed-loop structure of intelligent policy system for wireless channels allocation of IA (information appliance). At first, an approximated mathematical model and optimality equations of dynamic programming is defined. Then, the optimal control policy for this model can be computed via the method of successive approximation. Based on this algorithm for computing optimal policy, we design an intelligent system with feedback control to regulate the allocation of limited wireless channels. This intelligent system will continuously detect the status of usage of wireless channels. Once the system parameters deviate the predefined threshold or the prioritized weight for any type of in-coming request needs to be adjusted, the recomputing mechanism will be activated. Then a new optimal control policy is figured out and saved in database for use. Such a feedback control mechanism ensures that the performance of IA will keep near to the optimal level from time to time.

Keywords: Information Appliance, Intelligent Policy System, Wireless Communication, Queueing Theory, Dynamic Programming

REFERENCES

[1] Courtois, P. J. and Scheys, G., “Minimization of the Total Loss Rate for Two Finite Queues in Series,” IEEE Transactions on Communications, Vol. 39, pp. 1651-1661 (1991).
[2] Davis, E., “Optimal Control of Arrivals to a Two-server Queueing System with Separate Queues,” Ph.D. Dissertation, Program of Operation Researches, North Carolina State University, U.S.A. (1977).
[3] Ephremides, A., Varaiya, P. and Walrand, J., “A Simple, Dynamic Routing Problem,” IEEE Transactions on Automatic Control, Vol. 25, pp. 690-693 (1980).
[4] Gelenbe, E., Mang, X. and Onvural, R., “Bandwidth Allocation and Call Admission Control in High-speed Network,” IEEE Communications Magazine, Vol. 35, pp. 122-129 (1997)
[5] Ghoneim, H. and Stidham, S., “Optimal control of arrivals to two queues in series,” European Journal of Operation Research, Vol. 21, pp. 399-409 (1985).
[6] Hajek, B., “Optimal Control of Two Interacting Service Stations,” IEEE Transactions on Automatic Control, Vol. 29, pp. 491-499 (1984).
[7] Ku, C. Y. and Jordan, S., “Access Control to Two Multiserver Loss Queues in Series,” IEEE Transactions on Automatic Control, Vol. 42, pp. 1017-1023 (1997).
[8] Kumar, P. R. and Varaiya, P. P., Stochastic Systems, Prentice-Hall (1986).
[9] Karlsson, G., “Capacity Reservation in ATM Networks,” Computer Communications, Vol. 19, pp. 180-193 (1996).
[10] Lee, T. -H., Lai, K. -C. and Duann, S. -T., “Design of a Real-time Call Admission Controller for ATM Networks,” IEEE/ACM Transactions on Networking, Vol. 4, pp. 758-765 (1996).
[11] Rosberg, Z., Varaiya, P. P. and Walrand, J. C., “Optimal Control of Service in Tandem Queues,” IEEE Transactions on Automatic Control, Vol. 27, pp. 600-610 (1982).
[12] Stidham, S. and Weber, R., ”Control of Service Rates in Cycles and Series of Queues,” Stat. Lab., University Cambridge, U.K. (1983).
[13] Stidham, S. and Weber, R., ”A Survey of Markov Decision Models for Control of Networks of Queues,” Queueing Systems, Vol. 13, pp. 291-314 (1993).
[14] Stidham, S., “Optimal Control of Admission to a Queueing System,” IEEE Transactions on Automatic Control, Vol. 30, pp. 705-713 (1985).
[15] Weber, R., ”On the Optimal Assignment of Customers to Parallel Servers,” Journal of Applied Probability, Vol. 15, pp. 406-413 (1978).
[16] Winston, W., ”Optimality of the Shortest-processing-time Discipline,” Journal of Applied Probability, Vol. 14, pp. 181-189 (1977).
[17] Zhang, R. and Phillis, Y. A., “Fuzzy Control of Arrivals to Tandem Queues with Two Stations,” IEEE Transactions on Fuzzy Systems, Vol. 7, pp. 361-367 (1999).