A Mutual Extension to Kalman Filter for Interpretation of the GPS Ambiguities

P. Sirish Kumar; V.B.S. Srilatha Indira Dutt

doi:10.6180/jase.202102_24(1).0009

A Mutual Extension to Kalman Filter for Interpretation of the GPS Ambiguities

Computer Science and Information Engineering

P. Sirish Kumar This email address is being protected from spambots. You need JavaScript enabled to view it.¹ and V.B.S. Srilatha Indira Dutt²

¹Department of Electronics Communication Engineering, Aditya Institute of Technology and Management, Tekkali 532201, India.
²Department of Electronics Communication Engineering, GITAM University, Visakhapatnam 530045, India.

Received: August 19, 2020
Accepted: September 4, 2020
Publication Date: February 1, 2021

Download Citation: ||https://doi.org/10.6180/jase.202102_24(1).0009

ABSTRACT

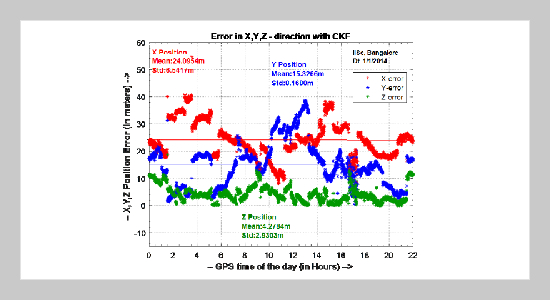
Some study methods, like least-squares, Kalman filter, are worked out so far to minimize this error factor and improve the GPS positioning accuracy. This paper presents a fast, accurate, and a new method in implementing Kalman Filter for GPS positioning, based on the correntropy criterion designated as the Correntropy Kalman Filter (CKF). The suggested model is evaluated using numerous 2-Dimensional and 3-Dimensional accuracy metrics in X, Y, Z directions. The proposed method results show that the positioning accuracy for all three co-ordinates is up to 34 %, significantly greater than the general approach (Traditional Kalman Filter).

Keywords: Accuracy; Correntropy; Correntropy Kalman Filter; Global Positioning System; Kalman Filter

REFERENCES

[1] David Rutledge. Innovation: accuracy versus precision. GPS World, 21(5):42–49, 2010.
[2] G S Rao. Global navigation satellite systems. Tata mcgra edition, 2010.
[3] R E Kalman. A New Approach to Linear Filtering and Prediction Problems 1. Technical report, 1960.
[4] Ramsey Faragher. Understanding the basis of the kalman filter via a simple and intuitive derivation [lecture notes]. IEEE Signal processing magazine, 29(5):128– 132, 2012.
[5] W Liu, PP Pokharel, JC Príncipe IEEE Transactions on Signal, and Undefined 2007. Correntropy: Properties and applications in non-Gaussian signal processing. ieeexplore.ieee.org, 55(11):5286–5298, 2007.
[6] Shokri, Sh, N. Rahemi and M. R. Mosavi. Improving GPS positioning accuracy using weighted Kalman Filter and variance estimation methods. CEAS Aeronautical Journal, pages 1–13, 2019.
[7] Badong Chen, Xi Liu, Haiquan Zhao, and Jose C. Principe. Maximum correntropy Kalman filter. Automatica, 76:70–77, feb 2017.
[8] RP Agarwal, M Meehan, and D O’regan. Fixed point theory and applications. Cambridge university press, 2001, 141, 2001.