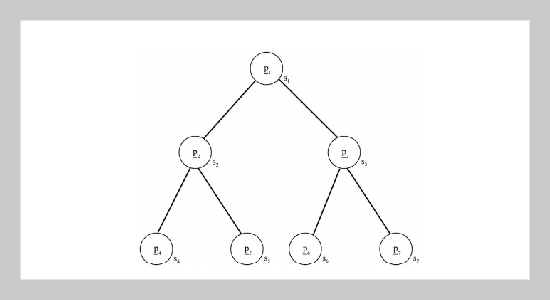
In this paper, a hierarchical particle swarm optimization (HPSO) is proposed to improve the premature convergence in the PSO approach. In the proposed HPSO approach, all particles are arranged in a regular tree structure and move up or down in the tree based on their fitness value. For the velocity update of each particle, it depends on the position of each particle in the tree. Besides, a mutation operator is added into the proposed HPSO approach. Consequently, the diversity of the population increases so that the HPSO approach can improve the premature convergence in the PSO approach. Finally, several benchmark functions for optimization problems are utilized to illustrate the effectiveness of the proposed HPSO approach to improving the premature convergence.
Keywords: Evolutionary Algorithm, Hierarchical Particle Swarm Optimization, Optimization Problem
REFERENCES
[1] Davis, L., Handbook of genetic algorithms, New York: Van Nostrand Reinhold (1991).
[2] Eberhart, R. and Kennedy, J., “A New Optimizer Using Particle Swarm Theory,” Proc. Int. Sym. Micro Machine and Human Science, Nagoya Japan, pp. 39 43 (1995).
[3] Kennedy, J. and Eberhart, R., “Particle Swarm Optimization,” Proc. IEEE Int. Conf. Neural Networks, Perth, Australia, pp. 19421948 (1995).
[4] Eshelman, L. J. and Schaffer, J. D., Real-coded genetic algorithms and interval schemata, Foundation of Genetic Algorithm-2. L. D. Whitley, ED. San Mateo, CA: Morgan Kaufmann (1993).
[5] Zhang, Q. and Leung, Y. W., “An Orthogonal Genetic Algorithm for Multimedia Multicast Routine,” IEEE Transactions Evolutionary Computation, Vol. 3, pp. 5362 (1999).
[6] Janson, S. and Middendorf, M., “A Hierarchical Particle Swarm Optimizer and Its Adaptive Variant,” IEEE Transactions on Systems, Man, and Cybernetics - Part B: Cybernetics, Vol. 35, pp. 12721282 (2005).
[7] Jian, W., Xue, Y. C. and Qian, J. X., “Improved Particles Swarm Optimization Algorithms Study Based on the Neighborhoods Topologies,” The 30th Annual Conference of the IEEE Industrial Electronics Society, Busan Korea, pp. 21922196 (2004).
[8] Krink, T., Vesterstrom, J. S. and Riget, J., “Particle Swarm Optimization with Spatial Particle Extension,” Proc. IEEE Congr. Evolutionary Computation (CEC 2002), pp. 14741479 (2002).
[9] Suganthan, P. N., “Particle Swarm Optimizer with Neighborhood Operator,” in Proc. Congr. Evolutionary Computation (CEC 1999), pp. 19581962 (1999).
[10] Ho, S. Y., Shu, L. S. and Chen, J. H., “Intelligent Evolutionary Algorithms for Large Parameter Optimization Problems,” IEEE Transactions on Evolutionary Computation, Vol. 8, pp. 522541 (2004).
[11] Lin, H. S., Design of a novel orthogonal particle swarm optimization. Master thesis, Feng Chia University, Taiwan, Republic of China (2004).
We use cookies on this website to personalize content to improve your user experience and analyze our traffic. By using this site you agree to its use of cookies.
